期权的风险及对冲
期权的“厚尾风险(Fat Tail Risk)”,也叫“极端风险”或“黑天鹅风险”,指的是标的资产在极短时间内出现极端价格变动(如暴涨或暴跌)时,期权组合所面临的巨大、非线性且不可预测的亏损风险。
什么是尾部风险(Tail Risk)
在金融统计中,资产收益分布通常不是完美正态的,而是厚尾分布,意味着极端事件虽然概率低,但一旦发生,影响极大且杀伤力强。
对于期权交易者来说:
- 卖方策略(如裸卖Put、Iron Condor、Strangle 等)虽然胜率高,但在尾部事件中可能遭遇灾难性亏损。
- 买方策略(如 Long Put、Straddle)则能利用后尾风险对冲或获利。
举例说明:
假设你卖出了一个 BTC 的 $80,000 Put(收取权利金 $1,000),当前价格 $100,000。你认为 BTC 不会这么快暴跌。
但如果出现市场崩盘:
- BTC 几天内跌至 $60,000
- 你需要以 $80,000 买入一枚 BTC,市价仅 $60,000
- 亏损 = $20,000 − $1,000 = $19,000
本来预期只赚 $1,000,最终暴亏近 20 倍 → 就是典型的“后尾风险”爆发。
后尾风险的表现形式:
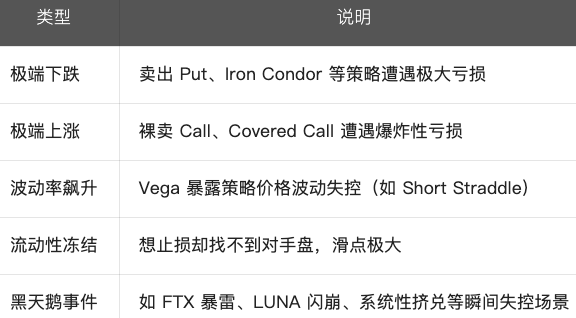
如何应对和管理后尾风险?
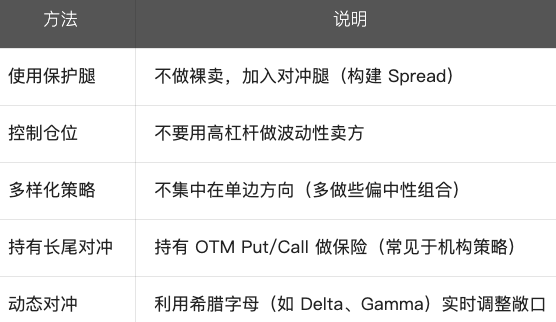
总结:
后尾风险是期权策略中极具破坏性的隐藏炸弹,尤其对卖方策略致命,不能靠“胜率高”来忽视风险暴露。真正稳定的期权交易,一定是在保护极端情境下仍能存活的策略体系。
什么是Whalley-Wilmott 渐进最优对冲模型(Asymptotic Optimal Hedging)
Whalley-Wilmott 模型是由 Paul Wilmott 和 Anne Whalley 提出的一种期权动态对冲(Dynamic Hedging)方法,主要用于最小化对冲成本的风险,特别是在交易成本(Transaction Costs)存在的情况下。该模型属于渐进最优(Asymptotically Optimal)对冲策略,适用于高频调整的对冲组合。
核心思想
在Black-Scholes模型中,理想情况下,期权卖方可以通过连续调整(Continuous Delta Hedging)完全对冲风险。但现实中:
- 交易成本(手续费、买卖价差)使得频繁调仓成本高昂。
- 离散对冲(Discrete Hedging)无法完全消除风险。
Whalley-Wilmott 模型的目标是:
在交易成本和风险之间找到最优平衡,即对冲频率不宜太高(避免成本过高),也不宜太低(避免风险暴露过大)。
关键公式
Whalley-Wilmott 给出了一个最优对冲区间(No-Trade Region),当标的资产价格超出该区间时,才进行调整:
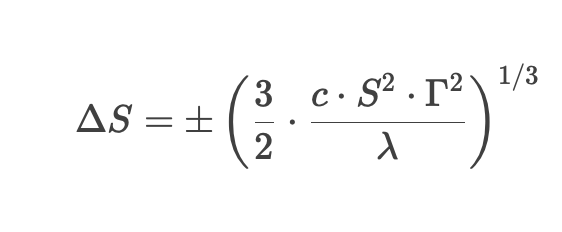
其中:
- ΔS = 触发对冲的价格变动阈值
- c = 交易成本(比例)
- S = 标的资产价格
- Γ = 期权的Gamma(二阶敏感度)
- λ = 风险厌恶系数(Risk Aversion)
策略规则:
1.计算当前期权的 Delta(对冲比例)。
2.设定一个容忍区间(No-Trade Region),只要资产价格在该区间内,不进行对冲。
3.当价格超出区间时,调整头寸使Delta回到目标值。
4.特点
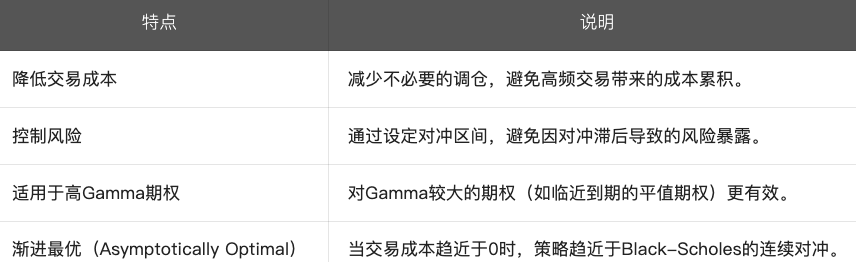
5.与其他对冲方法的对比

6.总结
- Whalley-Wilmott 模型 是一种考虑交易成本的动态对冲优化方法。
- 通过设定“不交易区间”(No-Trade Region),减少不必要的调仓,同时控制风险。
- 适用于高Gamma期权或高交易成本环境,是Black-Scholes模型的现实改进。
该模型在量化期权交易和风险管理中具有重要应用,尤其适合需要平衡交易成本和风险暴露的机构投资者。





