جذر ميركل

ما هو جذر ميركل؟

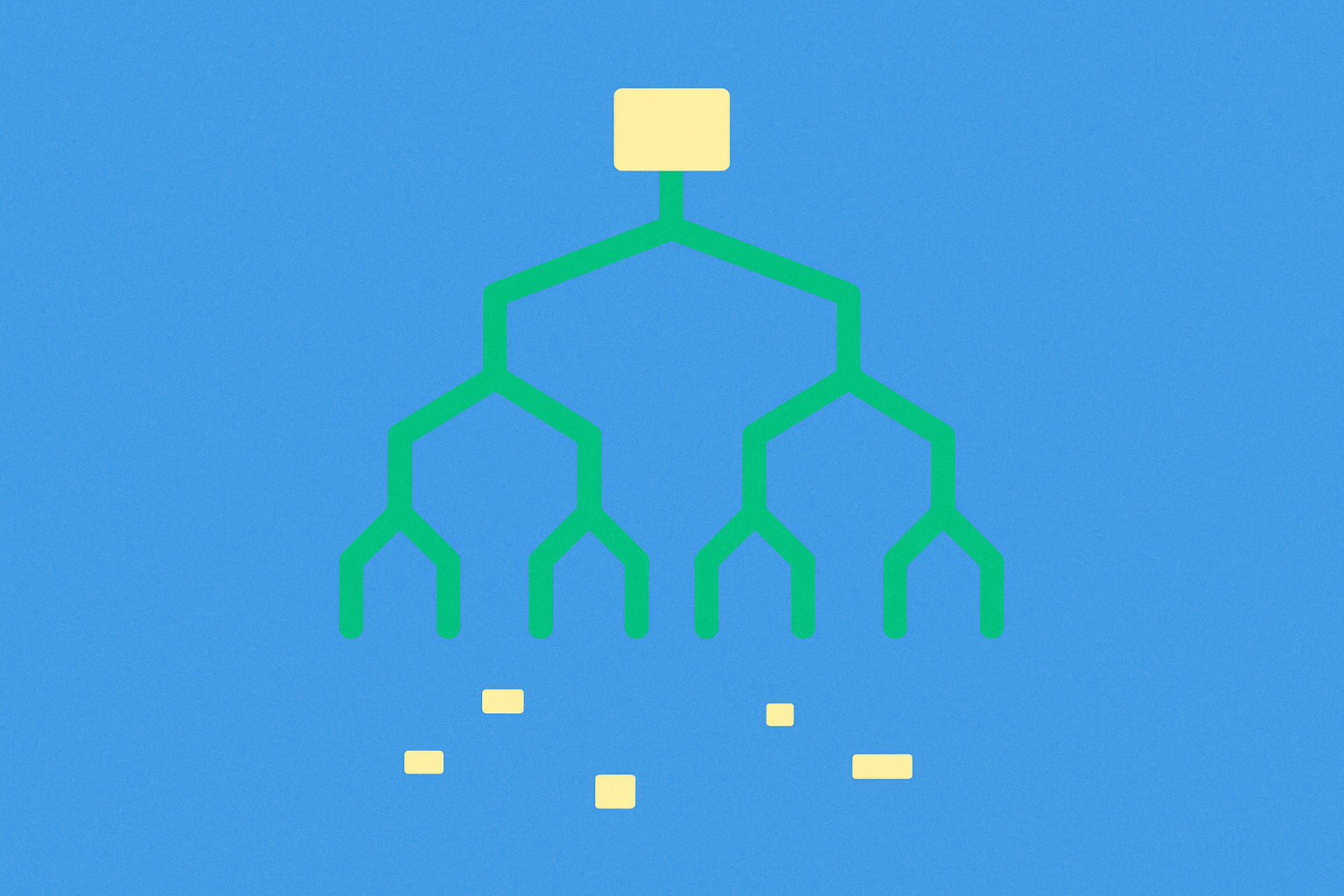
جذر ميركل هو تجزئة واحدة تلخص جميع المعاملات في الكتلة، يتم إنشاؤها من خلال دمج تجزئات المعاملات بشكل متكرر في بنية شجرية. تُخزن هذه التجزئة في رأس الكتلة وتعمل كملخص مضغوط للمعاملات المدرجة في الكتلة.

تشير "دالة التجزئة" هنا إلى خوارزمية تضغط بيانات عشوائية إلى بصمة بطول ثابت. أما "رأس الكتلة" فهو جزء من البيانات التعريفية يحتوي على عناصر مثل الطابع الزمني وتجزئة الكتلة السابقة وجذر ميركل، مما يساعد الشبكة على التحقق السريع من الكتل.

لماذا يعتبر جذر ميركل مهمًا في البلوكشين؟

جذر ميركل ضروري لأنه يتيح للمستخدمين التحقق مما إذا كانت معاملة معينة مدرجة في الكتلة دون الحاجة إلى تنزيل جميع المعاملات في تلك الكتلة. فكمية صغيرة من البيانات تكفي لإجراء التحقق، مما يسمح للعُقد الخفيفة—وهي عملاء يقومون بتنزيل رؤوس الكتل فقط—ومحافظ الهواتف المحمولة بالعمل بأمان مع موارد محدودة.

في Bitcoin، تعتمد آلية التحقق المبسط للدفع (SPV) على جذر ميركل. حيث تقوم المحافظ بتنزيل رأس الكتلة وتستخدم "مسار إثبات" قصير للمقارنة مع جذر ميركل لتحديد وجود المعاملة. بالنسبة للكتل التي تحتوي على آلاف المعاملات، يقلل ذلك بشكل كبير من متطلبات النطاق الترددي والتخزين.

وفقًا لإحصائيات مستكشفي الكتل العامة، فإن معظم كتل Bitcoin تتضمن عادة حوالي 1,000 إلى 3,000 معاملة حتى عام 2025 (المصدر: mempool.space، 2025-10). وعلى هذا النطاق، تبرز كفاءة استخدام جذور ميركل بشكل خاص.

كيف يتم حساب جذر ميركل؟

يتم حساب جذر ميركل بدمج تجزئات المعاملات صعودًا في شجرة ميركل حتى يتبقى تجزئة واحدة فقط.

الخطوة 1: حساب تجزئة المعاملة لكل معاملة. تجزئة المعاملة هي بصمة بطول ثابت يتم إنشاؤها عبر تجزئة بيانات المعاملة.

الخطوة 2: إقران تجزئات المعاملات المتجاورة، ودمجها (تسلسلها)، ثم تجزئة الناتج لتكوين تجزئة العقدة الأم. استمر في الدمج على شكل أزواج لبناء الطبقة التالية.

الخطوة 3: إذا كانت الطبقة تحتوي على عدد فردي من التجزئات (كما في Bitcoin)، يتم تكرار التجزئة الأخيرة لإكمال الاقتران—وقد تختلف التفاصيل بين شبكات البلوكشين.

الخطوة 4: كرر هذه العملية حتى يتبقى تجزئة واحدة في الأعلى. هذه التجزئة النهائية هي جذر ميركل. في Bitcoin، غالبًا ما تستخدم النتائج الوسيطة التجزئة المزدوجة (تطبيق دالة التجزئة مرتين) لزيادة مقاومة التصادم وهجمات تمديد الطول.

ما العلاقة بين جذر ميركل وشجرة ميركل؟

تنظم شجرة ميركل كميات كبيرة من البيانات على هيئة تجزئات في "شجرة ثنائية" هرمية. كل عقدة ورقية هي تجزئة معاملة، وكل عقدة أب هي تجزئة ناتجة عن دمج تجزئتي الابنين. جذر ميركل هو تجزئة الأب العليا لهذه الشجرة—ملخص يمثل جميع البيانات الأساسية.

يمكن تشبيه ذلك بمجلد: الأوراق هي بصمات الملفات الفردية، والطبقات العليا هي بصمات المجلدات الفرعية، وجذر ميركل هو البصمة الكلية للمجلد بأكمله. إذا تغيرت أي ورقة، تتغير جميع التجزئات العليا حتى الجذر، مما يجعله مؤشرًا موثوقًا على ما إذا تم تعديل مجموعة البيانات.

كيف يُستخدم جذر ميركل للتحقق من المعاملات؟

للتحقق مما إذا كانت معاملة معينة مدرجة في كتلة، يجب إعادة بناء "مسار الإثبات" من تلك المعاملة حتى جذر ميركل ومقارنته بجذر ميركل الموجود في رأس الكتلة.

الخطوة 1: الحصول على تجزئة المعاملة، ويمكن نسخها من المحفظة أو من صفحة تفاصيل المعاملة في مستكشف الكتل.

الخطوة 2: الحصول على إثبات ميركل—غالبًا ما يوفر مستكشفو الكتل سلسلة من "تجزئات المسار" (تجزئات الإخوة المجاورين لمعاملتك) للدمج عبر الطبقات.

الخطوة 3: دمج وتجزئة تجزئة المعاملة مع كل تجزئة مسار طبقة تلو الأخرى حتى الوصول إلى التجزئة العليا.

الخطوة 4: قارن التجزئة العليا المحسوبة بجذر ميركل للكتلة. إذا تطابقت، فإن معاملتك مؤكدة كجزء من تلك الكتلة.

عمليًا—على سبيل المثال أثناء عمليات الإيداع في Gate—تعرض صفحة التأكيد ارتفاع الكتلة وتوفر روابط لمستكشفي الكتل ذوي الصلة. يمكنك زيارة هذه الصفحات، والتحقق من جذر ميركل في رأس الكتلة، واستخدام هذه الخطوات للتحقق الذاتي.

الاختلافات بين جذور ميركل في Bitcoin وEthereum

في Bitcoin، يمثل جذر ميركل التجزئة العليا لشجرة ميركل ثنائية مبنية من جميع المعاملات ويُكتب في حقل "merkle root" في رأس الكتلة.

أما في Ethereum، فتحتوي رؤوس الكتل على عدة جذور: transactionsRoot (للمعاملات)، وstateRoot (للحالة العامة)، وreceiptsRoot (لإيصالات التنفيذ). ويتم بناء هذه الجذور باستخدام تراكيب "Merkle Patricia Trie"—وهي نسخة معدلة مناسبة لتخزين القيم حسب المفاتيح—مما يتيح حالات وفهارس أكثر تعقيدًا. وعلى الرغم من اختلاف آليات التنفيذ، إلا أن الهدف هو ضغط مجموعات بيانات ضخمة في ملخصات قابلة للتحقق.

يواصل المجتمع البحث عن تراكيب بيانات أكثر كفاءة—مثل أشجار Verkle—لتقليل حجم الإثبات وتكلفة المزامنة للعُقد الخفيفة. ومع ذلك، تظل التصاميم المعتمدة على ميركل مستخدمة على نطاق واسع لتوليد الملخصات والإثباتات القابلة للتحقق.

المخاطر والمفاهيم الخاطئة المرتبطة باستخدام جذور ميركل

أولًا، جذر ميركل يثبت فقط "سلامة مجموعة البيانات"؛ ولا يكشف مباشرة عن المعاملات الموجودة. يجب توفر إثبات ميركل وتجزئة المعاملة معًا لتأكيد الإدراج.

ثانيًا، تعتمد آلية SPV على الثقة في أن رؤوس الكتل المستلمة من السلسلة الرئيسية. قد تؤدي هجمات الشبكة (مثل العزل من قبل عُقد خبيثة) إلى تضليل المستخدمين مؤقتًا. ولهذا السبب، يجب الانتظار لعدد كافٍ من التأكيدات في العمليات المرتبطة بالأموال؛ حيث تتطلب منصات مثل Gate أعدادًا مختلفة من التأكيدات لكل سلسلة للحد من مخاطر الإنفاق المزدوج وإعادة التنظيم.

ثالثًا، تختلف تفاصيل التنفيذ بين شبكات البلوكشين—مثل ترتيب الدمج، ومعالجة الأوراق الفردية، وخوارزميات التجزئة، وصيغ الترميز. قد تؤدي الأخطاء في هذه العمليات إلى فشل التحقق.

رابعًا، تعتمد الأمان على مقاومة التصادم وعدم قابلية التلاعب لدوال التجزئة. وعلى الرغم من الاستخدام الواسع لخوارزميات التجزئة السائدة اليوم، إلا أن أي ثغرة في الخوارزمية ستقوض موثوقية جذر ميركل مباشرة.

كيف يمكن للمبتدئين عرض جذور ميركل في الأدوات؟

الخطوة 1: أدخل تجزئة المعاملة في مستكشف الكتل، وافتح صفحة تفاصيلها، وابحث عن الكتلة المقابلة، ثم انتقل إلى صفحة تلك الكتلة.

الخطوة 2: في قسم "رأس الكتلة" بصفحة الكتلة، ابحث عن الحقول مثل "merkle root" (في Bitcoin) أو "transactionsRoot/stateRoot/receiptsRoot" (في Ethereum). هذه الحقول هي الجذور الخاصة بكل نوع.

الخطوة 3: إذا تم توفير "Merkle Proof" أو "مسار الإثبات" في الصفحة، يمكنك استخدام الخطوات السابقة للحساب والمقارنة مع جذر ميركل للتحقق من المعاملة.

في صفحة سجلات الإيداع لدى Gate، يمكنك العثور على ارتفاع الكتلة لمعاملتك والوصول إلى صفحة مستكشف الكتل المقابلة لتحديد حقول رأس الكتلة وفهم كيفية عمل جذور ميركل بشكل أعمق.

الخلاصة: ما القيمة التي يوفرها فهم جذور ميركل؟

إتقان جذور ميركل يساعدك على فهم أسباب موثوقية الكتل، وآلية التحقق الخفيف في المحافظ، وكيفية اختيار السلاسل العامة لبنيتها البيانية. فمن خلال ضغط عدد كبير من المعاملات أو الحالات في ملخص واحد قابل للتحقق، تعزز جذور ميركل الكفاءة مع الحفاظ على حدود الأمان. وللمبتدئين، فإن معرفة كيفية استخدام جذور ميركل ومسارات الإثبات تمنحك القدرة على التحقق بثقة من الإيداعات والتحويلات والتفاعلات على الشبكة—وتقييم عدد التأكيدات والمخاطر بشكل أفضل.

الأسئلة الشائعة

لماذا تستطيع المحافظ الخفيفة التحقق من المعاملات باستخدام جذر ميركل فقط؟

المحافظ الخفيفة لا تحتفظ بجميع بيانات المعاملات لكل كتلة. فهي بحاجة فقط إلى جذر ميركل ومسار الإثبات للتحقق مما إذا تم التلاعب بمعاملة معينة—تمامًا مثل التحقق من الرمز الشريطي على طرد دون فتحه وفحص محتواه. يقلل ذلك بشكل كبير من متطلبات التخزين والنطاق الترددي للأجهزة المحمولة، مما يتيح محافظ جوال آمنة.

كيف يمكن أن يؤدي تغيير جذر ميركل إلى اختراق الكتلة بأكملها؟

يعمل جذر ميركل كبصمة إلكترونية للكتلة بالكامل. أي تلاعب حتى في معاملة واحدة يغيّر تجزئتها، وبالتالي تتغير جميع التجزئات العليا حتى جذر ميركل. هذا التأثير المتسلسل يمكّن جميع عُقد الشبكة من اكتشاف التعديلات فورًا. ويُعد هذا التصميم أساس قدرة البلوكشين على مقاومة التلاعب—وهو ركيزة أمنها.

لماذا يُستخدم شجرة ميركل بدلًا من دمج جميع تجزئات المعاملات مباشرة؟

دمج جميع تجزئات المعاملات مباشرة سينتج سلسلة ضخمة يصعب تخزينها ومقارنتها. أما التسلسل الثنائي في شجرة ميركل فيضغط التعقيد بشكل كبير في تجزئة جذرية بطول ثابت. يضمن ذلك التحقق الفعال لأي عدد من المعاملات دون زيادة زمن التحقق بشكل خطي مع عدد المعاملات.

هل يمكن خداع محافظ SPV بالاعتماد على جذور ميركل للتحقق؟

الاعتماد فقط على جذر ميركل المقدم من عقدة واحدة يحمل مخاطرة؛ إلا أن محافظ SPV عادةً ما تطلب جذور ميركل لنفس الكتلة من عدة عُقد مستقلة للمقارنة. طالما أن معظم العُقد صادقة، فإن تزوير جذر ميركل زائف أمر بالغ الصعوبة. هذا التوازن العملي بين الأداء والأمان مناسب لسيناريوهات الدفع اليومية.

لماذا يجب على المُعدنين إعادة حساب جذر ميركل أثناء التعدين؟

كلما اختار المُعدنون مجموعات مختلفة من المعاملات لإدراجها في كتلة جديدة، يتغير جذر ميركل—مما يؤدي بدوره إلى تغيير تجزئة رأس الكتلة. يواصل المُعدنون تعديل ترتيب المعاملات وقيم nonce بحثًا عن تجزئات تحقق متطلبات صعوبة الشبكة؛ وخلال هذه العملية، يعد إعادة حساب جذر ميركل أمرًا إلزاميًا. تضمن هذه الآلية معالجة المُعدنين لمحتوى المعاملات والتحقق منه فعليًا.